实验12:RLC串联谐振电路
RLC串联谐振电路
目标
1.理解电路发生谐振的条件、特点,掌握电路品质因数(Q值)、通频带的物理意义及其测定方法
2.学习用实验方法绘制RLC串联电路不同Q值下的幅频特性曲线
仪器仪表
| 仪器 | 元器件 | 工具 |
|---|---|---|
| ADALM2000 | - 5Ω 电阻(1/4W)×1 | - 面包板 |
| 数字万用表 | - 10mH 电感(1W)×1 | - 导线 |
| - 1μF 电容×1 |
仿真工具
Circuit JS
理论
含有两种不同储能性质元件的电路,在某一频率的正弦激励下,可以产生谐振。谐振分为串联谐振和并联谐振,它们均在电子电路中有着广泛的应用。本实验重点介绍RLC串联谐振电路。 在图1所示的RLC串联电路中,电路的复阻抗:
当符合下式时:
电路发生串联谐振,其特点是:Z=R,且为最小值,同时与同相,谐振频率:
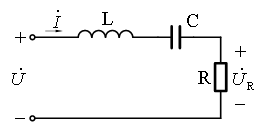
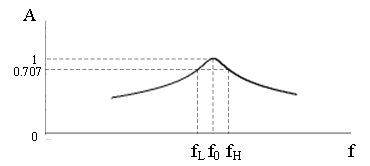
在图1电路中,以为激励信号,为响应信号,其幅频特性曲线如图2所示。在f = 时,A = /U = 1, = U;f ≠ 时, < U,呈带通特性。
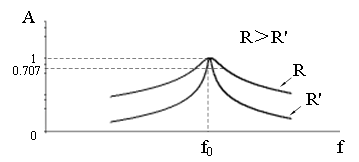
A = 0.707,即 = 0.707U所对应的两个频率和分别为下限频率和上限频率, - 为通频带。通频带的宽窄与电阻R有关,不同电阻值的幅频特性曲线如图3所示。
电路发生串联谐振时, = U, = = ,Q称为品质因数,与电路的参数R、L、C有关。Q值越大,幅频特性曲线越尖锐,通频带越窄,电路的选择性越好。在恒压源驱动时,电路的品质因数、选择性与通频带只决定于电路本身的参数,而与信号源无关。在本实验中,测量不同频率下的电压U、、和,绘制RLC串联电路的幅频特性曲线,由f = - 计算通频带,根据Q = /U = UC /U或Q = / - 计算品质因数。
Circuit JS仿真
调节信号源的频率,得到谐振频率,也可以通过公式计算得出。
实验
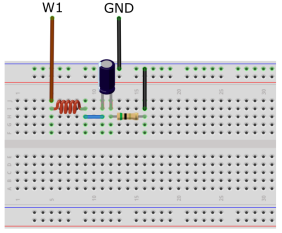
实验电路如图1所示。图中:L = 10mH,R、C可选不同数值,信号源选择正弦波电压作为输入电压u,使用ADALM2000提供正弦波电压,调节信号源正弦波电压的有效值U = 1V。
1.测量RLC串联电路的幅频特性
选取R = 5Ω,C = 1μF。对R的端电压进行AC扫描,得到RLC串联电路的幅频特性。适当选取扫描范围,使得到的幅频特性易于观察。
2.测量RLC串联电路谐振频率
在得到的幅频特性上测量电路的谐振频率,并记录该频率。
调整信号源的频率,使其等于谐振频率。测量电阻R的端电压,此时的读数应为最大值( = U = 1V)。若的读数不符,可适当调整信号源频率使之符合,此时的频率值即为电路的,并测量此时的与值,将测量数据记入数据表格中。
练习
设计一个具有增益的带通滤波器,其增益(放大倍数)A = 10,下限频率和上限频率分别为 = 100Hz和 = 100kHz。参考电路如图4所示,确定元件参数(选 = 100kΩ, = 10kΩ, = 10kΩ)。
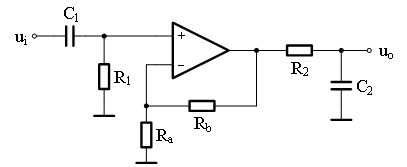
参考答案:由同向放大电路,可计算得出=90kΩ由C=,得出=16nF,=637pF。
Circuit JS仿真: